✅作者简介：热爱后端语言的大学生，CSDN内容合伙人
✨精品专栏：C++面向对象
🔥系列专栏：算法百炼成神

文章目录

• 🔥前言
• 1、AB3 有效括号序列
• • 1.1、解题思路
  • 1.2、代码实现与解析
• 2、AB4 逆波兰表达式求值
• • 2.1、解题思路
  • 2.2、代码实现与解析
• 3、AB5 点击消除
• • 3.1、解题思路
  • 3.2、代码实现与解析

🔥前言

本专栏收录的均为牛客网的算法题目，内含链表、双指针、递归、动态规划、基本数据结构等算法思想的具体运用。牛客网不仅有大量的经典算法题目，也有大厂的面试真题，面试、找工作完全可以来这里找机会。此外，网站内的编码主题多样化，调试功能可运用性强，可谓是非常注重用户体验。这么好的免费刷题网站还不快入手吗，快去注册开启算法百炼成神之路吧！

1、AB3 有效括号序列

题目链接：有效括号序列

题目描述：

1.1、解题思路

采用右括号入栈的思想：

1. 对s字符串进行遍历，如果是字符'('、'['、'{'那就把其对应的右括号入栈。
2. 如果不是这些左括号，那就让该字符与辅助栈顶比较，如果不相等说明不匹配：
   • 这里要先判断辅助栈是否为空，若为空，说明先前没有左括号入栈。
3. 如果字符与辅助栈顶相等，那就进行出栈操作，最后返回栈的empty方法即可。

1.2、代码实现与解析

本题源码：

class Solution {  public:    /**     *     * @param s string字符串     * @return bool布尔型     */    bool isValid(string s) {    //辅助栈 stack<char> stk; for (int i = 0; i < s.length(); i++) {     if (s[i] == '(')  stk.push(')');     else if (s[i] == '[')  stk.push(']');     else if (s[i] == '{')  stk.push('}');     else {  if (stk.empty() || s[i] != stk.top())      return false;      stk.pop();  } } return stk.empty();    }};

重要注释：

• 辅助栈需要字符型char，因为单个字符串可当作字符处理
• 如果遍历字符串是三种左括号，那就将对应右括号入栈
• 如果是右三种括号，判断栈是否为空或者是否与栈顶相等，不满足则出栈
• 如果empty方法为真，足以说明该字符串满足括号匹配

2、AB4 逆波兰表达式求值

题目链接：逆波兰表达式求值

题目描述：

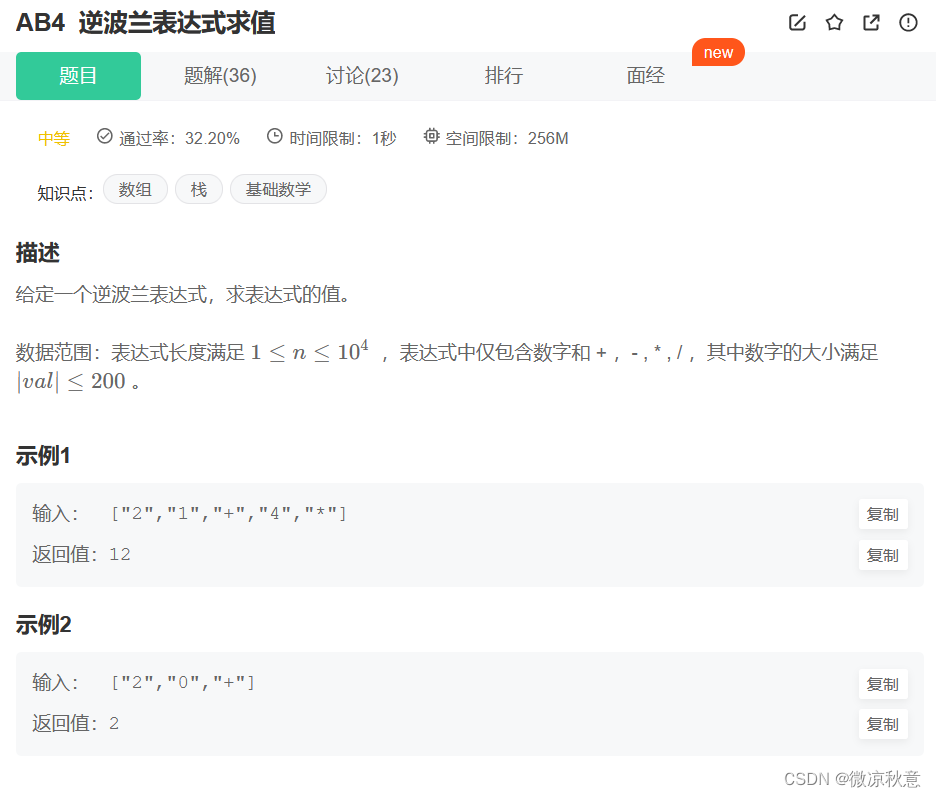
2.1、解题思路

所谓逆波兰表达式就是：操作数在前，操作符在后， 2 - 1 相当于2 1 -，采用辅助栈：

1. 遍历字符串，如果对应的字符不等于四则运算符，将操作数入栈
2. 如果字符为四则运算符，取栈顶后出栈再取栈顶，根据运算符将不同运算结果入栈
3. 遍历结束后的栈顶元素就是逆波兰表达式最终结果

2.2、代码实现与解析

本题源码：

class Solution {  public:    /**     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可     *     *     * @param s string字符串vector     * @return int整型     */    int evalRPN(vector<string>& s) { stack<int> stk; for (int i = 0; i < s.size(); i++) {     if (s[i] == "+" || s[i] == "-" || s[i] == "*" || s[i] == "/") {  int x1 = stk.top();  stk.pop();  int x2 = stk.top();  stk.pop();  if (s[i] == "+") stk.push(x1 + x2);  if (s[i] == "-") stk.push(x2 - x1);  if (s[i] == "*") stk.push(x1 * x2);  if (s[i] == "/") stk.push(x2 / x1);     } else {  stk.push(stoi(s[i]));     } } return stk.top();    }};

重要注释：

• 非四则运算符的话将字符串转化为整型后入栈，stoi可用于将字符型转化为整型
• 取栈顶后需要出栈一次才能再次取栈顶，这样才是两个连续的操作数
• 进行减法和除法时要让第二个栈顶在前，记住栈先进后出的特点

3、AB5 点击消除

题目链接：点击消除

题目描述：

3.1、解题思路

简单来说就是将相邻且相同的字符消除，采用辅助栈即可：

1. 辅助栈空时直接入栈
2. 后续遍历时若栈顶元素与之相等就出栈，不等就入栈
3. 判断最终栈的情况：
   • 若栈空，输出0
   • 若栈不空，输出栈内字符串

3.2、代码实现与解析

本题源码：

#include #include using namespace std;int main() {    string s, res;    cin >> s;    stack<char>stk;    for (int i = 0; i < s.size(); i++) { if (!stk.empty() && stk.top() == s[i]) {     stk.pop(); } else {     stk.push(s[i]); }    }    if (stk.empty()) cout << 0;    else { while (!stk.empty()) {     res = stk.top() + res;     stk.pop(); } cout << res;    }}

重要注释：

• 此题是自己设计输入输出，使用辅助栈需要包含头文件：
• 由于栈是先进后出，因此采用字符串拼接：res = stk.top() + res来得到正序字符串
• 核心点在于入栈和出栈的条件，这点掌握就没问题了

欢迎大家订阅专栏，学习算法思想，合理利用牛客网，百炼成神！

旅游攻略大全