👦👦一个帅气的boy，你可以叫我Love And Program
🖱 ⌨个人主页：Love And Program的个人主页
💖💖如果对你有帮助的话希望三连💨💨支持一下博主

SymPy 库

• 前言
• SymPy 基操
• 初中部分
• 高数部分
• • 微分方程
  • 极限

前言

SymPy 库是一个非常神秘的库，可以完成很多高数上的操作，以后我终于不怕做高数题咯🤪🤪

SymPy 基操

       先来个基本的除法练练手，evalf函数可以保留5位数字，Rational函数可以处理有理数。

from sympy import Rational#处理有理数r1 = Rational(1/3)r2 = Rational(1/3)val = (r1 + r2 ) * 4print(val.evalf(5))val2 = (1/3 + 1/3 ) * 4print(val2)#2.6667#2.6666666666666665

Mul是相乘，其中evaluate属性有延迟效果。

from sympy import sqrt, pprint, Mulx = sqrt(2)y = sqrt(3)pprint(Mul(x,  y, evaluate=False))print('结果为',x * y)#√6#结果为 sqrt(6)from sympy import expand, pprintfrom sympy.abc import xexpr = (x + 1) ** 3pprint(expr)print('*******************')#将其扩展开expr = expand(expr)pprint(expr)#3#(x + 2) #*******************# 3      2    #x  + 6⋅x  + 12⋅x + 8

这个库比正常直接计算更为精确，而且pprint函数还有修饰作用，更为直观的在程序中感受数学的魅力，欲听后事如何，咱们下面继续讲😁

然后...猜猜我在`Mul`函数中还发现什么？

       源码中这几个公式是不是很熟悉，小学学的乘法交换律，分配率？！哈哈，有点怀念哦，不行，简单了，让我们上上强度，小学数学跳跳，上初中。

初中部分

       顺延上面的公式，用solve函数求解，第一个参数是公式，第二个参数是需要解决的符号，于是单个变量的公式都可以用代码轻松计算。

#3#(x + 2) from sympy import Symbol, solvex = Symbol('x')expr = (x + 2) ** 3sol = solve(expr, x)print(sol)#结果：[-2]

还有一种方法也可以求解，Eq用于公式，下面求的是一个(x+2)^2=4的公式

#2    #(x + 2)  = 4from sympy import Symbol, solvex = Symbol('x')eq1 = Eq((x + 2) ** 2, 4)sol = solve(eq1, x)print(sol)#结果：[-4, 0]

那两个变量呢？

当然也可以

from sympy import symbols, solvex,y = symbols('x y')eq1 = Eq((x + 2) ** 2+y, y)pprint(eq1)sol = solve(eq1, x)print(sol)#    2    #y + (x + 2)  = y#[-2]

肯定会有人想y=x会是啥样，自己试试去🤪咱们接着上强度，高数上

高数部分

微分方程

上强度前我先问问大家，微分方程相关的科目学的咋样，我先来我先来，高数89，线代61，勉强过关吧，嘿嘿。既然如此，那...先来个微分方程试试水？。

先来一个二阶常系数齐次线性微分方程求解：

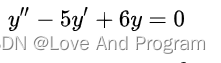
from sympy import Symbol, symbolsfrom sympy.abc import x, yf=Function('f')print(dsolve(Derivative(f(x),x,x)-5*Derivative(f(x),x)+6*f(x),f(x)))#Eq(f(x), (C1 + C2*exp(x))*exp(2*x))

       Derivative函数是求导，Derivative(f(x),x,x)意思为f(x)对x求两次导数，dsolve函数则是对f(x)求微分（可微即可导，可导不一定可微😏熟悉不）

上述结果如下，和代码结果是一样的。

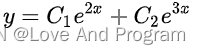
是不是感觉还不错，再来一道？！

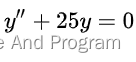
两次求导，加函数本身,得出结果。

from sympy import Symbol, symbolsfrom sympy.abc import x, yf=Function('f')print(dsolve(Derivative(f(x),x,x)+25*f(x),f(x)))#Eq(f(x), C1*sin(5*x) + C2*cos(5*x))

结果与代码一致

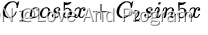
极限

最后来个极限收收尾吧~~

来看看下面几个题。

1、直接带入法

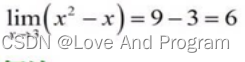
在sympy 库中有专门的极限函数limit，也有专门代表极限的函数oo，然后解函数吧。

from sympy import sin, limit, oofrom sympy.abc import xl2 = limit(x**2-x, x, 3)print(l2)#6

2、因式分解法

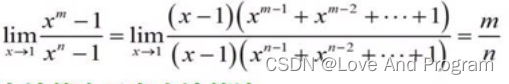
from sympy import limit, oo, symbolsfrom sympy.abc import xm,n = symbols('m n')l2 = limit((x**m-1)/(x**n-1), x, 1)print(l2)#m/n

3、概念判断法

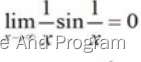
from sympy import sin, limit, oo, symbolsfrom sympy.abc import xm,n = symbols('m n')l2 = limit((1/x)*(sin(1/x)), x, oo)print(l2)#0

4、洛必达求导法

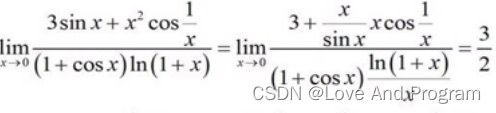
from sympy import cos, limit, oo, symbols, lnfrom sympy.abc import xm,n = symbols('m n')l2 = limit((3*sin(x)+((x**2)*cos(1/x)))/((1+cos(x))*ln(x+1)), x, 0)print(l2)#3/2

文章到这就结束了，SymPy完全用 Python 编写，只依赖于mpmath，比较容易上手，没事可以来试试实现高级算法公式，提升提升自己能力哦，就是这样。